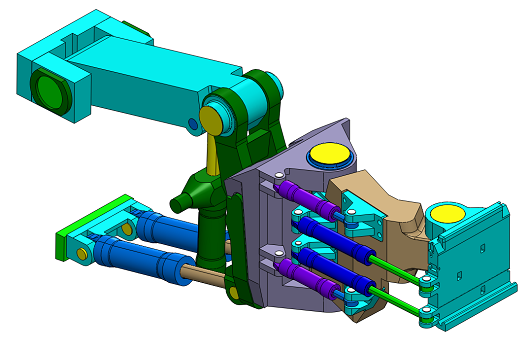
Fig.1 Maintenance robot, a flexible multibody system

Introduction

Flexible multibody systems are traditionally modeled by superimposing a rigid body motion and relative deformations, where the dependent variables include rigid body variables and relative deformation variables. This superimposed method is widely used but suffers some difficulties when applied to the modeling of geometric nonlinearities. In this formulation, constraint equations and mass matrix are very complicated and highly coupled between the rigid body and deformation variables.

Therefore, we have chosen a competing method that is based on a non-linear finite element, where dependent variables are measured by means of an inertial frame. As the finite element method (FEM) has widely expanded its notability in computational fluid dynamics and electromagnetics, it is expected that non-linear FEM will be the leading solving strategy for flexible multibody mechanics in the coming years.

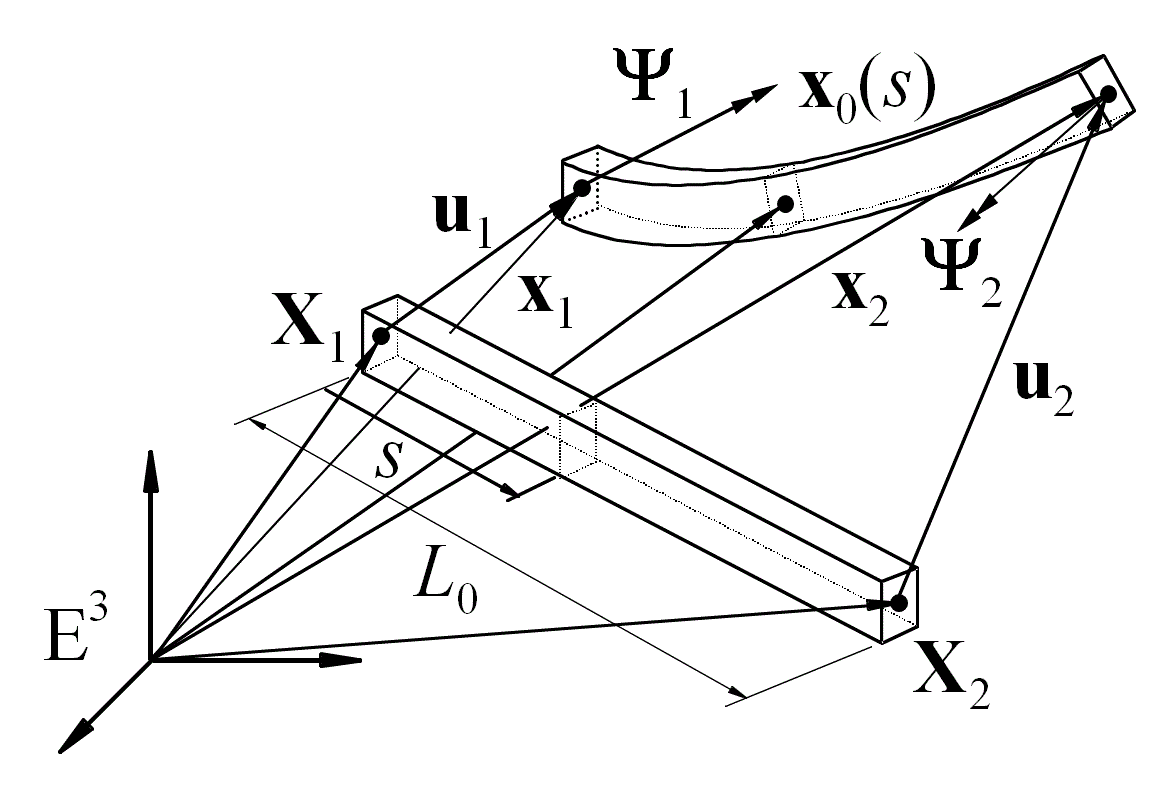
We have taken the geometrically exact approach over the fundamental beam hypothesis because the geometrically exact approach involves no other kinematic assumptions. In geometrically exact beam elements the placement field is measured with respect to an inertial frame and no corotational frames are included. This yields a more complicated stiffness matrix but a very simple mass matrix and the constraint equations. Especially, flexible translational joint where the joint follows the beam central line has a rather simple form.

We have introduced a new Reissner’s geometrically exact beam element that is based on a total Lagrangian updating procedure. The element has the total rotation vector as a dependent variable and the singularity problems at rotation angle 2π and its multiplies are passed by the change of parametrization on the rotation manifold SO(3). This beam element is presented in the thesis.

Fig. 2 Reissner's beam element in initial configuration and in deformed state

Research Personnel

Heikki Marjamäki, M.Sc., Dr.Tech.

Jari Mäkinen, M.Sc., Dr.Tech.

Antti Ylinen, M.Sc.

Previous projects:

The Analysis and Optimization of Flexible Mechanisms

The project is funded by the Natural Sciences and Engineering Research Council of the Academy of Finland

The aim of this project was to continue the scientific research, which our group has been carried out in analyzing flexible mechanisms using a nonlinear finite element method. In addition, the research field was expanded into optimization of the flexible mechanisms.

In this project, consistent coupling of the hydraulic system and mechanical system was studied and a method based on the nonlinear finite element analysis to solve the construction machine stability is evolved. Also the optimization and especially the sensitivity analysis of flexible multibody systems was studied.

Modelling and Simulation of Coupled Problems in Mechanics and Electrical Engineering (KOMASI)

The project was funded by Tekes, the Finnish Funding Agency for Technology and Innovation.

The project dealt with the development of computational techniques for the simulation of problems in multiphysics. The aim was to develop efficient methods for large and coupled problems. The following problems have been studied: contact mechanics, large structural deformations, nonlinear fracture mechanics, magnetostrictive materials and surface integral formulations in electromagnetics.

Teaching

Two Special Courses in Mechanics has been lectured since 2005 and dealt with modelling flexible multibody systems with nonlinear finite element method.

The post-graduate book seminars: